Standart Sapma Hesaplama

Enter Inputs	5,20,40,80,100 Enter the Numbers with Comma separated(,)

Result:
No.of Inputs
Mean
Standard Deviation(SD)
Population Standard Deviation(PSD)
Variance(SD)
Variance(PSD)
Calculation

Bir veri setinin yayılmasının ortak ölçüsünü hesaplamak için standart sapma hesaplayıcısı, bu bir veri analizidir. Hesap makinesi, verilerin, ortalama, standart sapma (SD), popülasyon standart sapması (PSD), varyans (SD), Nüfus Standart Sapma (PSD), Varyans (SD), Varyans (PSD) verileri verebilir.

Standart sapma formülü

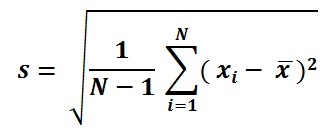
Standard Deviation Formula & Calculation

Nüfus SD Formülü

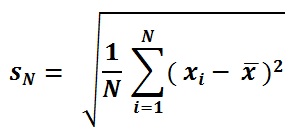
PSD - Population Standard Deviation Formula & Calculation

Varyans formülü

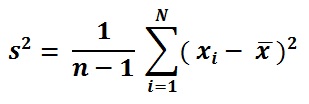
Variance Formula & Calculation

Ortalama formül

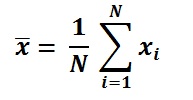
Mean Formula & Calculation

Örneğin, bir veri seti verildiğinde 5,20,40,80,100 , sonuç şudur:

Toplam girişler (n) = (5,20,40,80,100)

Toplam Girişler (n) = 5

Ortalama (xm) = (x1 + x2 + x3 ... xn) / n

Ortalama (xm) = 245/5

Anlamına gelir (xm) = 49

-------------------------------------------

Sd =

SQRT (1 / (n-1) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 + .. + (xn-xm) ^ 2))

= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 ))

= SQRT (1/4 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/4 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1605)

= 40.0625

Varyans = sd ^ 2

Varyans = 40.0625 ^ 2

Varyans = 1605

-------------------------------------------

Psd =

SQRT (1 / (n) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 + .. + (xn-xm) ^ 2))

= SQRT (1 / (5) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2))

= SQRT (1/5 (((((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/5 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1284)

= 35.8329

Varyans = sd ^ 2

Varyans = 35.8329 ^ 2

Varyans = 1284

Standart Sapma Hesaplama

FoxCalculators - Ücretsiz Çevrimiçi Hesap Makineleri!